Discrete Mathematics

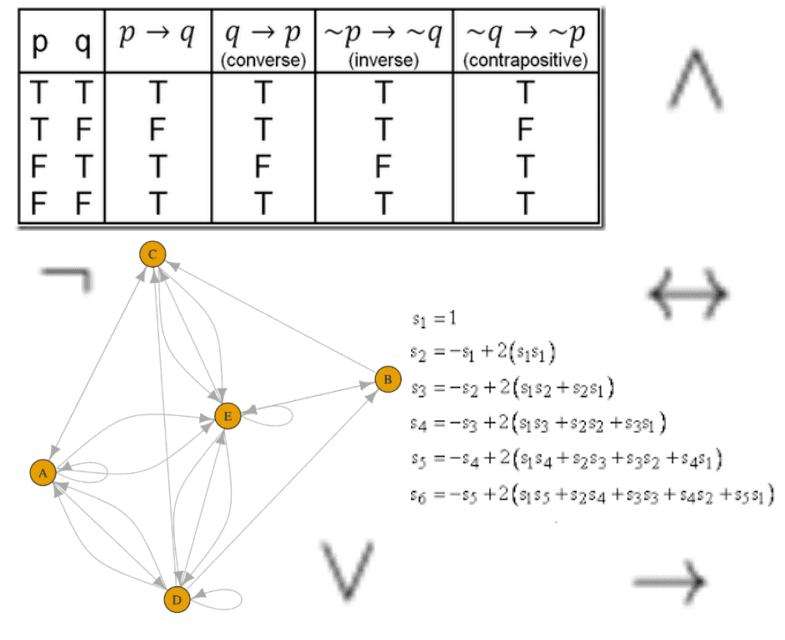
The second round of math at NTU was Discrete Math. This module was more about logical operations than calculations.

Some of the topics taught in this module were logical and, or, not, xor operations and solving expressions using their properties; truth tables, recurrence equations and graphs. They also touched a bit on Euler paths/circuits and Hamilton paths/circuits. These were slightly more complex concepts than the others but were interesting nonetheless!

This course was one of the easier modules as it quite simple to pick up and understand the concepts. But the downside of this module was that there was a lot of scope for twisting the questions. The questions were usually worded differently from the tutorials and tested multiple concepts together to increase the complexity. The final exam of Discrete Math was the epitome of this as the questions were deceptively simple and demanded deeper knowledge of the concepts.

This is something I had not realized until I started solving the past exam papers for this subject. The questions seemed so easy at first glance but when I got to solving them they were much more than that. I realized the burning need to further understand the concept than just the formulas given in the notes. I needed to solve more "application-based" questions to support the direct ones in the tutorials. This led to more internet research and reading on the topics until I was in a position to be able to solve the even the twisted questions.

From this module I was able to appreciate the need for attention to detail and how important it is to go beyond superficial learning.

I also scored an A grade for this module which gave me the opportunity to solve my paper again and submit the solution as a guide to the next batch of students taking this module.